Wikisage, the free encyclopedia of the second generation, is digital heritage
Ooosterschelde conicals
Jump to navigation
Jump to search
This article is an essay authored by
User:Franciscus[1]
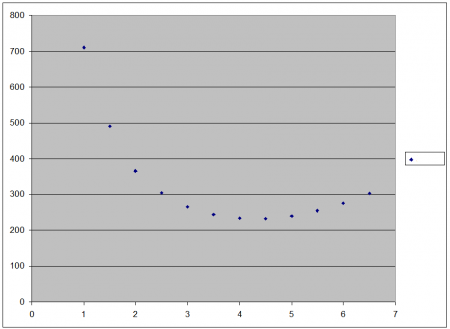
In Oosterschelde there is a cone with a very special property. It appears namely that when larger or smaller are out of the radius R - at a given content V - not just the surface area A becomes larger or smaller, but that also a smallest surface is present, or in other words: It achieves surface - at a constant content - a limit by changing the radius and height.
-
arrows shows a minimum
This proposition naturally ask for further clarification.