Wikisage, the free encyclopedia of the second generation and digital heritage, wishes you merry holidays and a happy new year!
Ooosterschelde conicals: Difference between revisions
Jump to navigation
Jump to search
(user?) |
No edit summary |
||
| Line 1: | Line 1: | ||
<small>[[File:Essay pen.jpg|32px]]This article is an essay authored by | <small>[[File:Essay pen.jpg|32px]]This article is an essay authored by | ||
[[User: | [[User:Franciscus]]<ref>http://nl.wikisage.org/w/index.php?title=Over_het_minimum_oppervlak_van_een_kegel&oldid=206429</ref> | ||
</small><br | </small><br | ||
[[File:Kugel-Zeeland.jpg|thumb|450px]] | [[File:Kugel-Zeeland.jpg|thumb|450px]] | ||
| Line 11: | Line 11: | ||
This proposition naturally ask for further clarification. | This proposition naturally ask for further clarification. | ||
</references> | |||
Revision as of 04:46, 17 November 2016
This article is an essay authored by
User:Franciscus[1]
<br
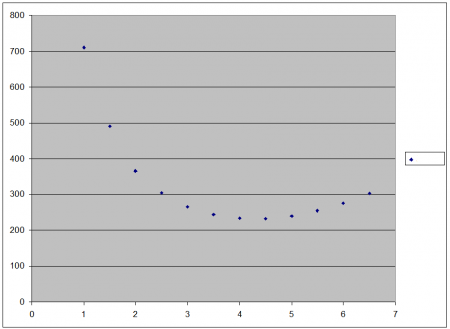
In Oosterschelde there is a cone a very special property. It appears namely that when larger or smaller are out of the radius R - at a given content V - not just the surface area A becomes larger or smaller, but that also a smallest surface is present, or in other words: It achieves surface - at a constant content - a limit by changing the radius and height.
-
arrows shows a minimum
This proposition naturally ask for further clarification. </references>