Wikisage, the free encyclopedia of the second generation and digital heritage, wishes you merry holidays and a happy new year!
Ooosterschelde conicals: Difference between revisions
Jump to navigation
Jump to search
mNo edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
[[File:Kugel-Zeeland.jpg|thumb|450px]] | [[File:Kugel-Zeeland.jpg|thumb|450px]] | ||
[[File:Areal radius relationship.png|thumb|450px]] | |||
In Oosterschelde there is a cone a very special property. | In Oosterschelde there is a cone a very special property. | ||
It appears namely that when larger or smaller are out of the radius R - at a given content V - not just the surface area A becomes larger or smaller, but that also a smallest surface is present, or in other words: It achieves surface - at a constant content - a limit by changing the radius and height. | It appears namely that when larger or smaller are out of the radius R - at a given content V - not just the surface area A becomes larger or smaller, but that also a smallest surface is present, or in other words: It achieves surface - at a constant content - a limit by changing the radius and height. | ||
This proposition naturally ask for further clarification. | This proposition naturally ask for further clarification. | ||
Revision as of 04:33, 17 November 2016

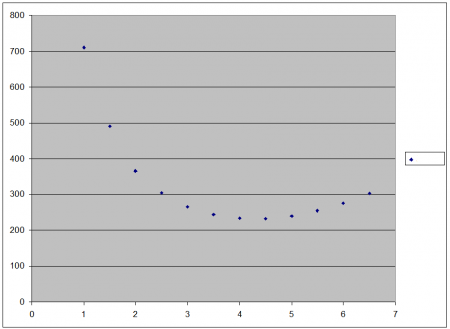
In Oosterschelde there is a cone a very special property. It appears namely that when larger or smaller are out of the radius R - at a given content V - not just the surface area A becomes larger or smaller, but that also a smallest surface is present, or in other words: It achieves surface - at a constant content - a limit by changing the radius and height. This proposition naturally ask for further clarification.