Wikisage, the free encyclopedia of the second generation and digital heritage, wishes you merry holidays and a happy new year!
Ooosterschelde conicals: Difference between revisions
Jump to navigation
Jump to search
mNo edit summary |
mNo edit summary |
||
| Line 5: | Line 5: | ||
In Oosterschelde there is a cone a very special property. | In Oosterschelde there is a cone a very special property. | ||
It appears namely that when larger or smaller are out of the radius R - at a given content V - not just the surface area A becomes larger or smaller, but that also a smallest surface is present, or in other words: It achieves surface - at a constant content - a limit by changing the radius and height. | It appears namely that when larger or smaller are out of the radius R - at a given content V - not just the surface area A becomes larger or smaller, but that also a smallest surface is present, or in other words: It achieves surface - at a constant content - a limit by changing the radius and height. | ||
<gallery>File:Grafiek_kegel_ohne_Titel.jpg</gallery> | <gallery>File:Grafiek_kegel_ohne_Titel.jpg|arrows shows a minimum</gallery> | ||
This proposition naturally ask for further clarification. | This proposition naturally ask for further clarification. | ||
Revision as of 04:35, 17 November 2016

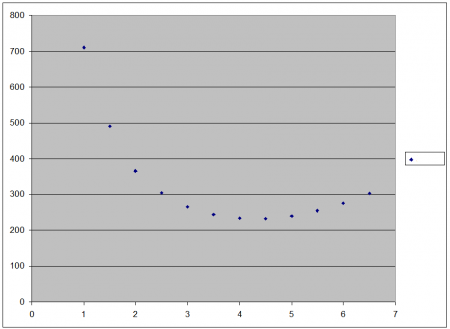
In Oosterschelde there is a cone a very special property. It appears namely that when larger or smaller are out of the radius R - at a given content V - not just the surface area A becomes larger or smaller, but that also a smallest surface is present, or in other words: It achieves surface - at a constant content - a limit by changing the radius and height.
-
arrows shows a minimum
This proposition naturally ask for further clarification.
